Կարգ՝ Ֆունկցիաներ

Արդիացված՝ Հունիսի 06 2022

Տրված է {jatex}f(x)=x|x-4|{/jatex} ֆունկցիան։

1․ Հաշվել ֆունկցիայի արժեքը {jatex}x=\sqrt 2 + 2{/jatex} կետում։

2․ Քանի՞ հատման կետ ունեն {jatex}y=5{/jatex} ուղիղը և {jatex}f{/jatex} ֆունկցիայի գրաֆիկը։

3․ Գտնել ֆունկցիայի մեծագույն արժեքը {jatex}[1; 2,5]{/jatex} միջակայքում։

4․ Գտնել {jatex}a{/jatex} պարամետրի ամբողջ արժեքների քանակը, որոնց դեպքում {jatex}y=a{/jatex} ուղիղը {jatex}f{/jatex} ֆունկցիայի գրաֆիկը հատում է ճիշտ երեք կետում։

Լուծում։

1․ {jatex}f(x)=x|x-4|{/jatex}

{jatex}f\left( 2+\sqrt 2 \right)=\left( 2+ \sqrt 2 \right) \left| 2+ \sqrt 2 - 4 \right| ={/jatex}

{jatex}=\left( 2+\sqrt 2 \right) \left| \sqrt 2 - 2 \right|{/jatex}

Քանի որ {jatex}y=\sqrt x {/jatex} ֆունկցիան աճող է, ուրեմն {jatex}\sqrt 2 < \sqrt 4{/jatex}, ուրեմն {jatex}\sqrt 2 < 2{/jatex}, ուրեմն {jatex}\sqrt 2-2<0{/jatex}, ուրեմն {jatex}\left| \sqrt 2 - 2 \right|=2-\sqrt 2{/jatex}:

{jatex}f \left( 2+\sqrt 2 \right) = \left( 2+\sqrt 2 \right) \left( 2-\sqrt 2\right)=2^2-2=2{/jatex}

2. {jatex}f{/jatex} ֆունկցիայի և {jatex}y=5{/jatex} ուղղի հատման կետերը գտնելու համար լուծենք {jatex}f(x)=5{/jatex} հավասարումը։

{jatex}f(x)=5{/jatex}

{jatex}x|x-4|=5{/jatex}

{jatex}\left[ \begin{aligned}
& \left\{ \begin{aligned}
& x-4 \geq 0 \\
& x(x-4)=5
\end{aligned} \right. \\
& \left \{ \begin{aligned}
& x-4 <0 \\
& x(-x+4)=5
\end{aligned}\right.
\end{aligned} \right. \quad{/jatex}{jatex}\left[ \begin{aligned}
& \left\{ \begin{aligned}
& x \geq 4 \\
& x^2-4x-5=0
\end{aligned} \right. \\
& \left \{ \begin{aligned}
& x<4 \\
& x^2-4x+5=0
\end{aligned}\right.
\end{aligned} \right. \quad{/jatex}

Լուծենք առանձին

1․ {jatex}x^2-4x-5=0{/jatex}

{jatex}D=16-4\cdot 1 \cdot (-5)=36{/jatex}

{jatex}\large x_1= \frac {4-6}{2}=-1 \quad x_2= \frac {4+6}{2}=5{/jatex}

{jatex}x \in  \left\{-1; 5 \right\}{/jatex}

2. {jatex}x^2-4x+5=0{/jatex}

{jatex}D=16-4\cdot 1 \cdot 5=-4{/jatex}

{jatex}x \in \emptyset{/jatex}

Տեղադրենք

{jatex}\left[ \begin{aligned}
& \left\{ \begin{aligned}
& x \geq 4 \\
& x \in \left\{ -1; 5 \right\}
\end{aligned} \right. \\
& \left \{ \begin{aligned}
& x<4 \\
& x \in \emptyset
\end{aligned}\right.
\end{aligned} \right. \quad{/jatex}{jatex}\left[ \begin{aligned}
& x \in \{ 5 \} \\
& x \in \emptyset
\end{aligned} \right.{/jatex}

{jatex}x \in \{ 5 \}{/jatex}

Ստացվեց, որ {jatex}f{/jatex} ֆունկցիան և {jatex}y=5{/jatex} ուղիղը հատվում են մեկ կետում, որի աբսցիսն է {jatex}x=5{/jatex}-ը։

3. Գտնենք {jatex}f{/jatex} ֆունկցիայի կրիտիկական կետերը, որոնք գտնվում են {jatex}[1; 2,5]{/jatex} հատվածում։

Եթե {jatex}x \in [1; 2,5]{/jatex}, ապա {jatex}x-4<0{/jatex}, ուրեմն {jatex}[1; 2,5]{/jatex} հատվածում 

{jatex}f(x)=x(-x+4)=-x^2+4x{/jatex}

{jatex}f'(x)=-2x+4{/jatex}, որը իմաստ ունի {jatex}[1; 2,5]{/jatex} հատվածում։

{jatex}f'(x)=0{/jatex}

{jatex}-2x+4=0{/jatex}

{jatex}x=2{/jatex}, որը պատկանում է {jatex}[1; 2,5]{/jatex} միջակայքին և որը որոշման տիրույթի ներքին կետ է, ուրեմն տրիտիկական կետ է։

 Այժմ հաշվենք {jatex}f{/jatex} ֆունկցիայի արժեքը {jatex}[1; 2,5]{/jatex} հատվածի ծայրակետերում և կրիտիկական կետերում։

{jatex}f(1)=1(-1+4)=3{/jatex}

{jatex}f(2)=2(-2+4)=4{/jatex}

{jatex}f(2,5)=2,5(-1,5+4)=3,75{/jatex}

{jatex}\max \limits_{[1;2,5]}=f(2)=4{/jatex}

4. Գտնենք {jatex}f{/jatex} ֆունկցիայի կրիտիկական կետերը։

{jatex}D(f)=(- \infty ; + \infty){/jatex}

{jatex}f'(x)= \left\{ \begin{aligned}
& 2x-4 \text{ եթե } x>4 \\
& -2x+4 \text{ եթե } x<4\\
& \text{իմաստ չունի, եթե } x=4
\end{aligned} \right.{/jatex}

{jatex}x=4{/jatex}-ը որոշման տիրույթի ներքին կետ է, ուրեմն կրիտիկական կետ է։

{jatex}f'(x)=0{/jatex}

{jatex}\left[ \begin{aligned}
& \left\{ \begin{aligned}
& x>4 \\
& 2x-4=0
\end{aligned} \right. \\
& \left \{ \begin{aligned}
& x<4 \\
& -2x+4=0
\end{aligned}\right.
\end{aligned} \right. \quad{/jatex}{jatex}\left[ \begin{aligned}
& \left\{ \begin{aligned}
& x>4 \\
& x=2
\end{aligned} \right. \\
& \left \{ \begin{aligned}
& x<4 \\
& x=2
\end{aligned}\right.
\end{aligned} \right. \quad{/jatex}{jatex}\left[ \begin{aligned}
&  x\in \emptyset \\
& x=2
\end{aligned} \right. \quad{/jatex}

{jatex}x=2{/jatex}, որը որոշման տիրույթի ներքին կետ է, ուրեմն կրիտիկական կետ է։

{jatex}D(f){/jatex}-ը կրիտիկական կետերով տրոհենք միջակայքերի և որոշենք ածանցյալի նշանը նրանցից յուրաքանչյուրում։

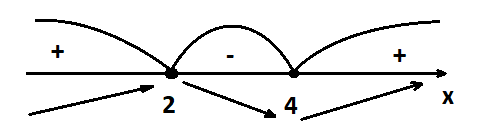
{jatex}f'(0)=-2 \cdot 0 +4=4>0{/jatex}

{jatex}f'(3)=-2 \cdot 3+4=-2<0{/jatex}

{jatex}f'(5)=2\cdot 5-4=2>0{/jatex}

{jatex}x_{max}=2 \quad x_{min}=4{/jatex}

{jatex}y_{max}=f(2)=2|2-4|=4 \quad y_{min}=4|4-4|=0{/jatex}

Ստացված արդյունքները բավական են {jatex}f{/jatex} ֆունկցիայի գրաֆիկի կառուցման համար։

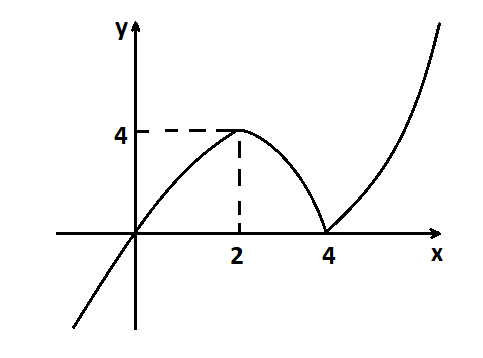
Ստացված գրաֆիկից երևում է, որ {jatex}y=a{/jatex} ուղիղը կհատի {jatex}y=f(x){/jatex} ֆունկցիայի գրաֆիկին երեք կետում, եթե {jatex}0<a<4{/jatex}:

Այդ պայմանին բավարարող ամբողջ թվերը կլինեն 1; 2; 3 թվերը՝ քանակը կլինի երեք հատ։

Պատասխան՝ 2; 1; 4; 3։

Կարգ՝ Ֆունկցիաներ

Արդիացված՝ Հունիսի 05 2022

Տրված է {jatex}f(x)=-x^2+3x+4{/jatex} ֆունկցիան։

1․ Հաշվել {jatex}f'(3){/jatex}-ը։

2․ {jatex}f{/jatex} ֆունկցիայի գրաֆիկը քանի՞ հատման կետ ունի կոորդինատների առանցքների հետ։

3․ Գտնել {jatex}f{/jatex} ֆունկցիայի գրաֆիկի այն կետի աբսցիսը, որում նրա գրաֆիկին տարված շոշափողը զուգահեռ է {jatex}y=-9x+1{/jatex} ուղղին։

4․ Գտնել {jatex}a{/jatex} պարամետրի այն ամենափոքր բնական արժեքը, որի դեպքում {jatex}f{/jatex} ֆունկցիայի գրաֆիկն ամբողջովին գտնվում է {jatex}y=a{/jatex} ուղղից ներքև։

Լուծում։

1. {jatex}f(x)=-x^2+3x+4{/jatex}

{jatex}f'(x)=-2x+3{/jatex}

{jatex}f'(-3)=-2\cdot (-3)+3=9{/jatex}

2. Եթե {jatex}x=0 \quad f(x)=f(0)=4{/jatex}:

Եթե {jatex}f(x)=0{/jatex} 

{jatex}-x^2+3x+4=0{/jatex}

{jatex}D=9-4 \cdot (-1)\cdot 4=25{/jatex} 

{jatex}\large x_1= \frac{-3-5}{-2}=4 \quad x_2=\frac{-3+5}{-2}=-1{/jatex}

Առանցքների հետ հատման կետերը ստացվեցին {jatex}(0;4);(4;0);(-1;0){/jatex}:

Հատման կետերի քանակը ստացվեց 3։

3․ Որպեսզի շոշափողը լինի զուգահեռ {jatex}y=-9x+1{/jatex} ուղղին նախ հարկավոր է, որ

{jatex}f'(x)=(-9x+1)'{/jatex}

{jatex}-2x+3=-9{/jatex}

{jatex}-2x=-12{/jatex}

{jatex}x=6{/jatex}։

Այնուհետև հարկավոր է, որ {jatex}x=6{/jatex} կետում տարված շոշափողը չհամընկնի {jatex}y=-9x+1{/jatex} ուղղի հետ։

Արդեն հաշվել ենք, որ {jatex}f'(6)=-9{/jatex}:

Հաշվենք {jatex}f(6){/jatex}-ը․

{jatex}f(6)=-6^2+3\cdot 6+4=-14{/jatex}

{jatex}x=6{/jatex} կետում տարված շոշափողի հավասարումը կլինի․

{jatex}y=f'(6)(x-6)+f(6){/jatex}

{jatex}y=-9(x-6)-14{/jatex}

{jatex}y=-9x+40{/jatex}, որը չի համընկնում {jatex}y=-9x+1{/jatex} ուղղի հետ, ուրեմն {jatex}x=6{/jatex} կետում տարված շոշափողը իրոք զուգահեռ է {jatex}y=-9x+1{/jatex} ուղղին։

4․ Նախ գտնենք {jatex}E(f){/jatex}-ը։

Գտնենք բոլոր այն {jatex}b{/jatex}-երը, որոնց համար {jatex}f(x)=b{/jatex} հավասարումը ունի լուծում։

{jatex}-x^2+3x+4=b{/jatex}

{jatex}x^2-3x+b-4=0{/jatex}

{jatex}D=9-4(b-4)=25-4b{/jatex}

Որպեսզի հավասարումը ունենա լուծում, հարկավոր է, որ

{jatex}D \geq 0{/jatex}

{jatex}25-4b \geq 0{/jatex}

{jatex}4b \leq 25{/jatex}

{jatex}b \leq 6,25{/jatex}

{jatex}b \in ( -\infty ; 6,25]{/jatex}

{jatex}E(f)=(-\infty ; 6,25]{/jatex}

{jatex}a{/jatex} ամբողջ թվի համար {jatex}f{/jatex} ֆունկցիայի գրաֆիկը կլինի ամբողջությամբ {jatex}y=a{/jatex} ուղղից ներքև, եթե {jatex}a=7; 8; 9; ...{/jatex}:

Այդ թվերից ամենափոքրը 7-ն է։

Պատասխան՝ 9; 3; 6; 7։

Կարգ՝ Ֆունկցիաներ

Արդիացված՝ Հունիսի 05 2022

Տրված են {jatex}f(x)=\large \frac {100}{1+x^2}{/jatex} և {jatex}g(x)=x^2-4x+50{/jatex} ֆունկցիաները։

1․ Գտնել {jatex}f{/jatex} ֆունկցիայի մեծագույն արժեքը։

2․ Գտնել {jatex}g{/jatex} ֆունկցիայի փոքրագույն արժեքը։

3․ {jatex}f{/jatex} ֆունկցիայի արժեքների տիրույթը քանի՞ ամբողջ թիվ է պարունակում։

4․ {jatex}f{/jatex} և {jatex}g{/jatex} ֆունկցիաների արժեքների տիրույթները քանի՞ ընդհանուր ամբողջ թիվ են պարունակում։

Լուծում։

1․ Եթե {jatex}x=0 \quad f(x)=f(0)=\large \frac {100}{1+0^2}=100{/jatex}

 Եթե {jatex}x \neq 0{/jatex} ապա {jatex}x^2 >0{/jatex}

{jatex}x^2+1>1{/jatex} և քանի որ {jatex}y= \large \frac {100}{x}; (0; +\infty ){/jatex} ֆունկցիան նվազող է, ուրեմն

{jatex}\large \frac {100}{1+x^2}< \frac {100}1{/jatex}

{jatex}f(x)<100{/jatex}, ուրեմն

{jatex}\max f(x)= f(0)=100{/jatex}

2. {jatex}g(x)=x^2-4x+50=x^2-2\cdot 2x+2^2+46=(x-2)^2+46 \geq 46{/jatex}

{jatex}g(2)=46{/jatex}, ուրեմն

{jatex}\min g(x)=46{/jatex}

3. Գտնենք բոոր այն {jatex}a{/jatex}-երը, որոնց համար {jatex}f(x)=a{/jatex} հավասարումը ունի լուծում։

{jatex}f(x)=a{/jatex}

{jatex}{\large \frac{100}{1+x^2}}=a{/jatex}

{jatex}{\large \frac{100}{1+x^2}}-a=0{/jatex}

{jatex}{\large \frac {100-a\left(1+x^2 \right)}{1+x^2}}=0{/jatex}

Քանի որ {jatex}x^2 \geq 0{/jatex}, ուրեմն {jatex}1+x^2>0{/jatex}

{jatex}100-a\left( 1+x^2 \right)=0{/jatex}

{jatex}-ax^2+100-a=0{/jatex}

{jatex}ax^2=100-a{/jatex}

{jatex}a=0{/jatex} դեպքում {jatex}100-a=100{/jatex} և հավասարումը լուծում չի ունենա։

Որպեսզի հավասարումը ունենա լուծում հարկավոր է, որ {jatex}a \neq 0{/jatex} և {jatex}{\large \frac {100-a}{a}}\geq 0{/jatex}:

Կազմենք համակարգ։

{jatex}\left\{ \begin{aligned}
& a \neq 0 \\
& { \frac {100-a}{a}}\geq 0
\end{aligned} \right.{/jatex}

Լուծենք առանձին։

{jatex}\frac{100-a}{a} \geq 0{/jatex}

{jatex}x \in (0; 100]{/jatex}

Տեղադրենք

{jatex}\left\{ \begin{aligned}
& a \neq 0 \\
& x \in (0; 100]
\end{aligned} \right.{/jatex}

{jatex}a \in (0; 100]{/jatex}

{jatex}E(f)=(0; 100]{/jatex}, որում ամբողջ թվերն են 1; 2; 3; ․․․; 100, որոնց քանակը կլինի 100 հատ։

4․ Գտնենք {jatex}g(x){/jatex} ֆունկցիայի արժեքների տիրույթը։

Գտնենք բոլոր այն {jatex}b{/jatex}-երը, որոնց համար {jatex}g(x)=b{/jatex} հավասարումն ունի լուծում։

{jatex}g(x)=b{/jatex}

{jatex}x^2-4x+50=b{/jatex}

{jatex}x^2-4x+50-b=0{/jatex}

{jatex}D=16-4(50-b)=4b-184{/jatex}

Որպեսզի հավասարումն ունենա լուծում, հարկավոր է, որ {jatex}D \geq 0{/jatex}:

{jatex}D \geq 0{/jatex}

{jatex}4b-184 \geq 0{/jatex}

{jatex}4b \geq 184{/jatex}

 {jatex}b \geq 46{/jatex}

{jatex}b \in [46; + \infty ){/jatex}

{jatex}E(g)=[46; + \infty ){/jatex}

Գտնենք {jatex}E(f)=(0; 100]{/jatex} և {jatex}E(g)=[46;+\infty ){/jatex} բազմությունների հատումը։

{jatex}y \in [46; 100]{/jatex}

Քանի որ 1; 2; 3; ․․․; 100 թվերից այդ հատվածին չեն պատկանում 1; 2; 3; ․․․; 45 թվերը, {jatex}[46; 100]{/jatex} հատվածում ամբողջ թվերի քանակը կլինի հավասար 100-45=55:

Պատասխան՝ 100; 46; 100; 55։

Կարգ՝ Ֆունկցիաներ

Արդիացված՝ Հունիսի 05 2022

Տրված է {jatex}f(x)=\sqrt{30-5x^2}+26{/jatex} ֆունկցիան։

1․ Գտնել {jatex}f{/jatex} ֆունկցիայի մաքսիմումի կետը։

2․ Գտնել {jatex}f{/jatex} ֆունկցիայի գրաֆիկի {jatex}x_0=1,5{/jatex} աբսցիսն ունեցող կետում տարված շոշափողի և աբսցիսների առանցքի կազմած անկյան աստիճանային չափը։

3․ Գտնել {jatex}f{/jatex} ֆունկցիայի գրաֆիկի {jatex}x_0=-1{/jatex} աբսցիսն ունեցող կետվ տարված շոշափողի և կոորդինատային առանցքներով սահմանափակված պատկերի մակերեսը։

4․ Գտնել {jatex}f{/jatex} ֆունկցիայի գրաֆիկի այն կետի աբսցիսը, որում տարված շոշափողը զուգահեռ է {jatex}y=-x+\ln 2{/jatex} ուղղին։

Լուծում։

{jatex}f(x)= \sqrt{30-5x^2}+26{/jatex}

Գտնենք կրիտիկական կետերը

{jatex}30-5x^2 \geq 0{/jatex}

{jatex}6-x^2 \geq 0{/jatex}

{jatex}\left( \sqrt 6 - x \right) \left( \sqrt 6 + x \right) \geq 0{/jatex}

{jatex}x \in \left[- \sqrt 6 ; \sqrt 6 \right]{/jatex}

{jatex}f'(x)=\large \frac{\left( 30-5x^2 \right)'}{2\sqrt{30-5x^2}}={/jatex}

{jatex}=\frac {-10x}{2 \sqrt{30-5x^2}}=\frac{-5x}{\sqrt{30-5x^2}}{/jatex}

Ածանցյալը իմաստ չունի երբ {jatex}\sqrt{30-5x^2}=0{/jatex} կամ {jatex}30-x^2 <0{/jatex}:

Կազմենք համախումբ․

{jatex}\left[
\begin{aligned}
& \sqrt {30-5x^2}=0 \\
& 30-5x^2<0
\end{aligned} \right. \quad {/jatex}{jatex}\left[
\begin{aligned}
& 30-5x^2=0 \\
& 30-5x^2<0
\end{aligned} \right.{/jatex}

{jatex}30-5x^2 \leq 0{/jatex}

{jatex}6-x^2 \leq 0{/jatex}

{jatex}\left( \sqrt 6 - x \right) \left( \sqrt 6 + x \right) \leq 0{/jatex}

{jatex}x \in \left( - \infty ; -\sqrt 6\right] \cup \left[ \sqrt 6; + \infty \right) {/jatex}, որոնք {jatex}D(f){/jatex}-ի ներքին կետեր չեն, ուրեմն կրիտիկական կետեր չեն։

{jatex}f'(x)=0{/jatex}

{jatex}{\large \frac {-5x}{\sqrt{30-5x^2}}}=0{/jatex}

{jatex}\left\{ \begin{aligned}
& -5x=0 \\
& \sqrt{30-5x^2}\neq 0
\end{aligned} \right. \quad{/jatex}{jatex}\left\{ \begin{aligned}
& x=0 \\
& 30-5x^2 > 0
\end{aligned} \right.{/jatex}

Հատումը կատարենք ստուգման միջոցով։

Երբ {jatex}x=0{/jatex} համակարգի անհավասարման ձախ կողմը կլինի հավասար {jatex}30-5 \cdot 0^2=30{/jatex}:

{jatex}30>0{/jatex}-ն ճշմարիտ անհավասարություն է, ուրեմն {jatex}x=0{/jatex}-ն անհավասարման, ինչպես նաև համակարգի լուծում է։

{jatex}x=0{/jatex}-ն {jatex}D(f){/jatex}-ի ներքին կետ է, ուրեմն կրիտիկական կետ է։

Որոշման տիրույթը կրիտիկական կետով տրոհենք միջակայքերի և հաշվենք ածանցյալի նշանը նրանցից յուրաքանչյուրում։

{jatex}f'(-1)=\frac{5\cdot (-1)}{\sqrt{30-5(-1)^2}}=-1<0{/jatex}

{jatex}f'(1)=\frac {5 \cdot 1}{\sqrt{30-5\cdot 1}}=1>0{/jatex}

{jatex}x_{max}=0{/jatex}

2. {jatex}x_0=1,5{/jatex} աբսցիսն ունեցող կետում տարված շոշափողի {jatex}\varphi {/jatex} անկյունը, որտեղ {jatex}0^{\circ} \leq \varphi < 180^{\circ}{/jatex}, բավարարում է {jatex}tg \varphi =f'(1,5){/jatex} պայմանին։

{jatex}f'(1,5)= {\large \frac {-5 \cdot 1,5}{\sqrt{50-5\cdot(1,5)^2}}}={/jatex}

{jatex}={ \large -\frac{5\cdot 2 \cdot 1,5}{\sqrt{4\cdot 30-5\cdot 4 \cdot (1,5)^2}}= \frac{-15}{\sqrt{120-45}}=\frac {-15}{5\sqrt 3}= }-\sqrt 3{/jatex}

{jatex}tg \varphi =- \sqrt 3 \quad 0^{\circ}\leq \varphi < 180^{\circ}{/jatex}

{jatex}\varphi= 120^{\circ}{/jatex}

Պահանջվող աստիճանային չափը ստացվեց 120։

3․ {jatex}f(-1)=\sqrt{30-5\cdot (-1)^2}+26=31{/jatex}

{jatex}f'(-1)=\large \frac{(-5)(-1)}{30-5 \cdot 1^2}= \frac 5{\sqrt{25}}=1{/jatex}

{jatex}x_0=-1{/jatex} կետում տարված շոշափողի հավասարումը կլինի․

{jatex}y=f'(-1)(x+1)+f(-1){/jatex}

{jatex}y=1(x+1)+31{/jatex}

{jatex}y=x+32{/jatex}

Եթե {jatex}x=0{/jatex} ապա {jatex}y=32{/jatex}:

Եթե {jatex}y=0{/jatex} ապա {jatex}x=-32{/jatex}:

{jatex}y=x+32{/jatex} ուղղով և կոորդինատային առանցքներով սահմանափակված պատկերը կլինի ուղղանկյուն եռանկյուն, որի էջերը հավասար են 32-ի, ուրեմն մակերեսը կլինի հավասար {jatex}\frac 12 \cdot 32 \cdot 32=512{/jatex}:

4․ Որպեսզի տարված շոշափողը լինի զուգահեռ {jatex}y=-x+\ln 2{/jatex} ուղղին, նախ հարկավոր է, որ {jatex}f'(x)=(-x+ \ln 2 )'{/jatex}

{jatex}{\large \frac {-5x}{\sqrt{30-5x^2}}}=-1{/jatex}

{jatex}\left\{ \begin{aligned}
& -5x=-\sqrt{30-5x^2} \\
& \sqrt{30-5x^2}\neq 0
\end{aligned} \right. \quad{/jatex}{jatex}\left\{ \begin{aligned}
& \sqrt{30-5x^2}=5x \\
& \sqrt{30-5x^2}\neq 0
\end{aligned} \right. \quad{/jatex}{jatex}\left\{ \begin{aligned}
& 30-5x^2=25x^2\\
&5x \geq 0 \\
& 30-5x^2 >0
\end{aligned} \right. \quad{/jatex}{jatex}\left\{ \begin{aligned}
& x^2=1\\
& x \geq 0 \\
& 30-5x^2 >0
\end{aligned} \right. \quad{/jatex}{jatex}\left\{ \begin{aligned}
&x=1 \\
& 30-5x^2 >0
\end{aligned} \right. \quad{/jatex}

Համակարգի հատումը կատարենք ստուգման միջոցով։

Եթե {jatex}x=1{/jatex}, ապա անհավասարման ձախ մասից կստացվի {jatex}30-5\cdot 1^2=25{/jatex}, {jatex}25>0{/jatex}-ն ճշմարիտ անհավասարություն է, ուրեմն 1-ը համակարգի անհավասարման արմատ է, ուրեմն 1-ը համակարգի լուծում է։

Ցույց տանք, որ {jatex}x=1{/jatex} կետում տարված շոշափողը չի համընկնում {jatex}y=-x+\ln 2{/jatex} ուղղի հետ։

{jatex}f(1)=\sqrt{30-5 \cdot 1^2}+26=31{/jatex}

{jatex}f'(1)=\large \frac{-5 \cdot 1}{\sqrt{30-5\cdot 1^2}}=-1{/jatex}

{jatex}x=1{/jatex} կետում տարված շոշափողի հավասարումը կլինի․

{jatex}y=f'(1)(x-1)+f(1){/jatex}

{jatex}y=-1(x-1)+31{/jatex}

{jatex}y=-x+32{/jatex}, որը չի համընկնում {jatex}y=-x+ \ln 2{/jatex} ուղղի հետ։

Պատասխան՝ 0; 120; 512; 1։

Կարգ՝ Ֆունկցիաներ

Արդիացված՝ Հունիսի 02 2022

Տրված է {jatex}f(x)=x^3-6x^2+9x{/jatex} ֆունկցիան։

1․ Գտնել {jatex}f{/jatex} ֆունկցիայի զրոների քանակը։

2․ Գտնել {jatex}f{/jatex} ֆունկցիայի կրիտիկական կետերի քանակը։

3․ Գտնել {jatex}f{/jatex} ֆունկցիայի մինիմումի կետը։

4․ Գտնել {jatex}f{/jatex} ֆունկցիայի ամենամեծ արժեքը միջակայքում։

Լուծում։

{jatex}f(x)=0{/jatex}

{jatex}x^3-6x^2+9x=0{/jatex}

 {jatex}x \left( x^2 - 2\cdot 3x +3^2 \right)=0{/jatex}

{jatex}x(x-3)^2=0{/jatex}

{jatex}\left[ \begin{aligned}
& x =0 \\
& (x-3)^2 =0
\end{aligned} \right. \quad{/jatex}{jatex}\left[ \begin{aligned}
& x=0 \\
& x-3=0
\end{aligned} \right. \quad{/jatex}{jatex}\left[ \begin{aligned}
& x=0 \\
& x=3
\end{aligned} \right. \quad{/jatex}

{jatex}x \in \{ 0 ; 3 \}{/jatex}

Զրոների քանակը ստացվեց 2 հատ։

2․ {jatex}f(x)=x^3-6x^2+9x{/jatex}

Գտնենք կրիտիկական կետերը։

{jatex}D(f)=( - \infty ; + \infty ){/jatex}

{jatex}f'(x)=3x^2-12x+9{/jatex}, որը {jatex}D(f){/jatex}-ի բոլոր կետերում իմաստ ունի։

{jatex}f'(x)=0{/jatex}

{jatex}3x^2-12x+9=0{/jatex}

{jatex}x^2-4x+3=0{/jatex}

{jatex}D=16-4 \cdot 1 \cdot 3=4{/jatex}

{jatex}\large x_1= \frac {4-2}2=1 \quad x_2= \frac {4+2}2=3{/jatex}

 {jatex}x \in \{ 1 ; 3 \}{/jatex}, որոնք {jatex}D(f){/jatex}-ի ներքին կետեր են, ուրեմն կրիտիկական կետեր են։

Կրիտիկական կետերի քանակը ստացվեց 2 հատ։

3. {jatex}f{/jatex} ֆունկցիայի որոշման տիրույթը կրիտիկական կետերով տրոհենք միջակայքերի և որոշենք ածանցյալի նշանը նրանցից յուրաքանչյուրում։

{jatex}f'(0)=3 \cdot 0^2 -12 \cdot 0+9=9>0{/jatex}

{jatex}f'(2)=3\cdot 2^2- 12 \cdot 2 +9=-3<0{/jatex}

{jatex}f'(4)=3 \cdot 4 ^2-12 \cdot 4+9=9>0{/jatex}

{jatex}x_{min}=3, \quad x_{max}=1{/jatex}

Ֆունկցիայի մինիմումի կետը ստացվեց 3-ը։

4. Գտնենք {jatex}f{/jatex} ֆունկցիայի մեծագույն արժեքը [1; 5] հատվածում։ Այն հավասար է այդ հատվածի ծայրակետերի և կրիտիկական կետերի ֆունկցիայի արժեքներից մեծագույնին։

{jatex}f(1)=1-6+9=4{/jatex}

{jatex}f(5)=5^3-6\cdot 5^2+9 \cdot 5=20{/jatex}

Քանի որ {jatex}x=3{/jatex} կրիտիկական կետը մինիմումի կետ է, ուրեմն {jatex}\max  \limits_{[1;5]} f(x) \neq f(3){/jatex}:

{jatex}\max \limits_{[1; 5]}f(x) =f(5)=20{/jatex}

Պատասխան՝ 2; 2; 3; 20։

Կարգ՝ Ֆունկցիաներ

Արդիացված՝ Մայիսի 31 2022

Տրված է {jatex}f(x)=x+ \large \frac {27}{x^3}{/jatex} ֆունկցիան։

1․ Գտնել {jatex}f{/jatex} ֆունկցիայի մինիմումի կետը։

2․ Գտնել {jatex}f{/jatex} ֆունկցիայի էքստրեմումի արժեքներից մեծագույնը։

3․ Գտնել {jatex}f{/jatex} ֆունկցիայի գրաֆիկի {jatex}x_0=-3{/jatex} աբսցիսն ունեցող կետում տարված շոշափողի անկյունային գործակիցը։

4․ Գտնել {jatex}b{/jatex}-ի բոլոր ամբողջ արժեքների քանակը, որոնցից յուրաքանչյուրի դեպքում {jatex}y=b{/jatex} ուղիղը {jatex}f{/jatex} ֆունկցիայի գրաֆիկի հետ ընդհանուր կետ չունի։

Լուծում։

1. {jatex}f(x)=x+ \large \frac {27}{x^3}{/jatex}

Գտնենք կրիտիկական կետերը

{jatex}x^3 \neq 0{/jatex}

{jatex}x \neq 0{/jatex}

{jatex}x \in (- \infty ; 0) \cup (0 ; + \infty ){/jatex}

{jatex}D(f)= (- \infty ; 0) \cup (0; + \infty){/jatex}

{jatex}f'(x)=1- \large \frac {81}{x^4}{/jatex} որը իմաստ չունի, երբ

{jatex}x^4 =0{/jatex}

{jatex}x=0{/jatex}, որը {jatex}D(f){/jatex}-ի ներքին կետ չէ, ուրեմն կրիտիկական կետ չէ։

{jatex}f'(x)=0{/jatex}

{jatex}1- \large \frac {81}{x^4}=0{/jatex}

{jatex}\begin{cases}
& x^4-81=0 \\
& x^4 \neq 0
\end{cases} \quad {/jatex}{jatex}\begin{cases}
& x^4=81 \\
& x \neq 0
\end{cases} \quad{/jatex}{jatex}\begin{cases}
& x= \pm 3 \\
& x \neq 0
\end{cases}{/jatex}

{jatex}x= \pm 3{/jatex} որոնք {jatex}D(f){/jatex}-ի ներքին կետեր են, ուրեմն կրիտիկական կետեր են։

Որոշման տիրույթը կրիտիկական կետերով տրոհենք միջակայքերի և որոշենք ածանցյալի նշանը նրանցից յուրաքանչյուրում։

{jatex}f'(-4)=1- \large \frac {81}{(-4)^4}=1- \large \frac{81}{256} >0{/jatex}

{jatex}f'(-2)=1-\large \frac {81}{(-2)^4}=1- \large \frac {81}{16}<0{/jatex}

{jatex}f'(2)=1- \large \frac {81}{2^4}= 1-\large \frac {81}{16}<0{/jatex}

{jatex}f'(4)=1-\large \frac {81}{4^4}=1-\large \frac {81}{256}>0{/jatex}

{jatex}x_{min}=3 \quad x_{max}=-3{/jatex}

Մինիմումի միակ կետը ստացվեց 3-ը։

2․ {jatex}y_{min}=f(3)=3+\large \frac {27}{3^3}=4{/jatex}

{jatex}y_{max}=f(-3)=3+\large \frac {27}{(-3)^3}=-4{/jatex}

Էքստրեմումի կետերից մեծագույնը ստացվեց 4-ը։

3․ {jatex}f{/jatex} ֆունկցիայի {jatex}x_0=3{/jatex} աբսցիսն ունեցող կետում տարված շոշափողի անկյունային գործակիցը կլինի հավասար {jatex}f'(-3){/jatex}-ին։

{jatex}f'(-3)=1-\large \frac {81}{(-3)^4}=0{/jatex}

4. Արդեն գտել ենք էքստրեմումի կետերը, մոնոտոնության միջակայքերը։

Կառուցենք {jatex}f{/jatex} ֆունկցիայի գրաֆիկը։

Գրաֆիկից երևում է, որ {jatex}y=b{/jatex} ուղիղը չի հատի {jatex}f{/jatex} ֆունկցիայի գրաֆիկը, եթե {jatex}-4<b<4{/jatex}, որին բավարարող ամբողջ թվերն են -3; -2; -1; 0; 1; 2; 3։ Քանակը ստացվեց 7 հատ։

Պատասխան՝ 3; 4; 0; 7։